Conic Equations

SIT Conic Equations

Derivation of SIT Non Linear Algebraic Equations

From the ImageJ slit values, SIT computes the Y's - the differences between each zone pair slit images in inches. SIT nonlinear algebraic equations compute Yi as a function of Z (the Foucaults). Next Excel's Solver is used to find the value of Z such that the difference between Yi and Y is nearly zero. Then Sixtests or FigureXp can be used to compute the mirror surface from the Foucault's.

Mask tests are of two verities, Moving or Fixed Source. The Lateral Wire Test is a Moving Source test. SIT is a Fixed Source test where the camera and source are separated, and as such an exact solution is required rather than an approximation.

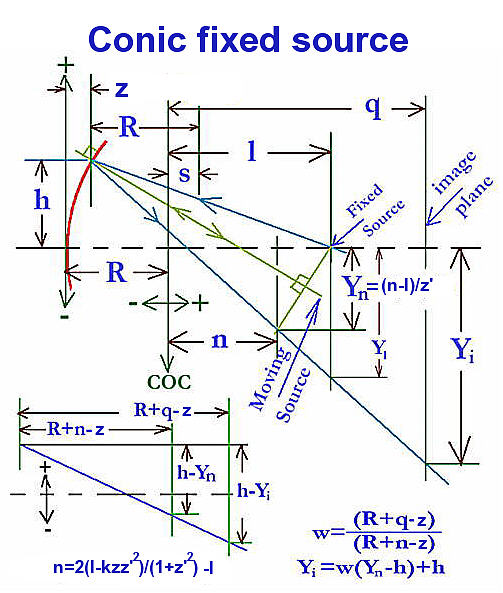
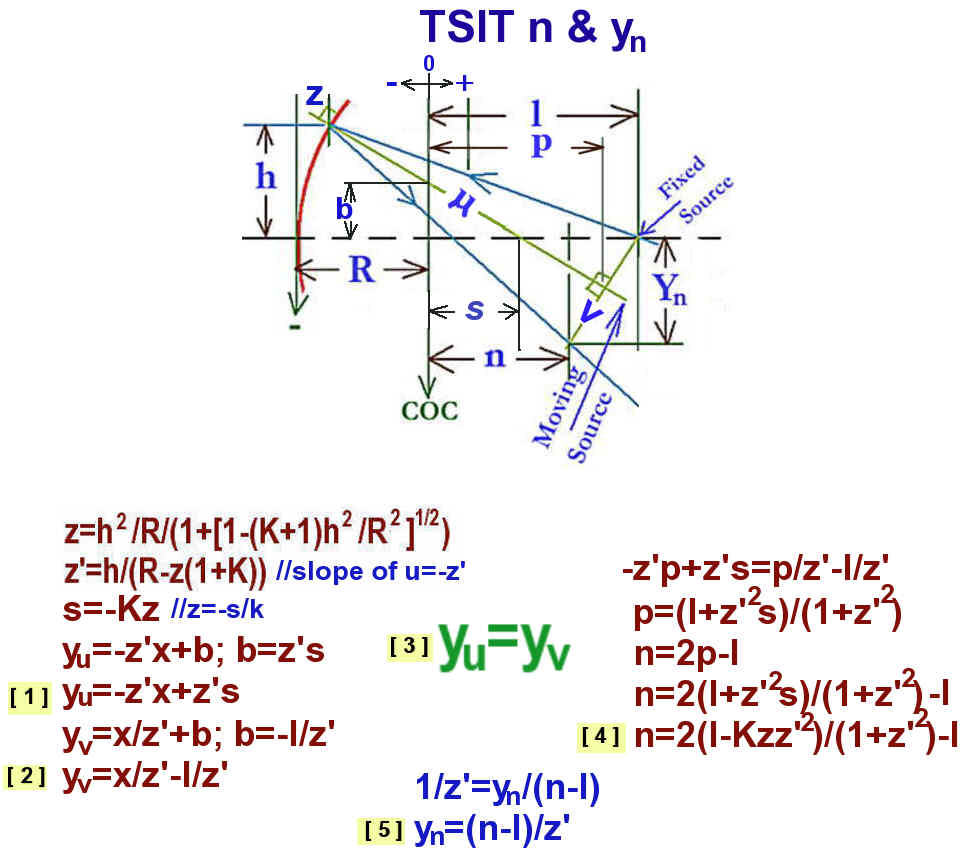
To compute the Yi of Fig: Conic fixed source need equations for variables n and Yn of Fig: SIT n and Yn. The derivation for n proceeds using the equation of a straight line y=mx+b where slope m is slope u, the normal to the conic surface (z') and b = z's. From this then, [1]: Yu=-z'x+z's. Next to compute Yv need to know the slope of v (the perpendicular to u), which is the inverse of the slope of u i.e., 1/z' (see proof below).

Then [2]: Yv=X/z'-l/z'. Next find the intersection of lines u and v which is the solution of the simultaneous equations Yv and Yu i.e., [3]: Yv=Yu, which leads to the solution [4]: n=2(l-Kzz'^2)/(1+z'^2)-l. And then knowing n, [5]: Yn=(n-l)/z'.

Now knowing n, and Yn, can solve for Yi of Fig: Conic fixed source if we knew z. From the Conic Equations z = Z/-K, where Z is the Foucault. As stated above, Excel's Solver is used to find the value of Z such that the difference between Yi and Y is nearly zero.

The sum of the angles in a triangle is 180 degrees. The angles in the two large right triangles are the same, being the sides are the same. Angles a and b of the small triangle are the same as that of the large right triangles. Therefore the small triangle is also a right triangle and the slopes (hypotenuses) are at right angles.